what is meant by quantisation
CLICK BELOW FOR TOTORIAL ON CONVOLUTION
www.fourier-series.com/fourierseries2/flash_programs/Convolution/index.html
click below to play a game in SS
www.fourier-series.com/fourierseries2/flash_programs/fourier_series_sin_cos/index.html
This subject is nothing but., Give INPUT get OUTPUT
Have a cool look on the topics on left
What do u want?
post below!

| Property Name | Illustration |
|---|---|
| Definition |
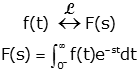 |
| Linearity |
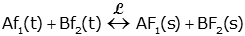 |
| First Derivative |
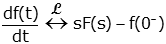 |
| Second Derivative |
 |
| nth Derivative |
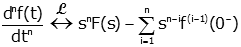 |
| Integration |
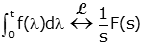 |
| Multiplication by time |
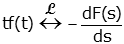 |
| Time Shift |
 |
| Complex Shift |
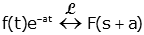 |
| Time Scaling |
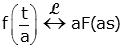 |
|
Convolution ('*' denotes convolution of functions) |
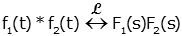 |
| Initial Value Theorem |
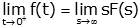 |
| Final Value Theorem |
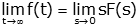 |
Topic: SS
Subject: ss By: prakash Date: 26/10/2012
Subject: SS By: sample Date: 15/10/2012
what is meant by sampling
Why do we use laplace transform?
The most generalized reason would be:
"To solve initial-valued differential equations of the 2nd (or higher) order." Laplace is a little powerful for 1st order, but it will solve them as well.
There is a limitation here: Laplace will only generate an exact answer if initial conditions are provided. Laplace cannot be used for boundary-valued problems.
In terms of electronics engineering, the Laplace transform is used to get your model into the s-domain, so that s-domain analysis may be performed (finding zeroes and poles of your characteristic equation).
This is particularly useful if one needs to determine the kind of response an RC, RLC, or LC circuit will provide (i.e. underdamped, overdamped, critically damped).
Once in the s-domain, we may begin discussing the components in terms of impedance. Sometimes it is easier to calculate the voltage or current across a capacitor or an inductor in terms of the components' impedances, rather than find it in a t-domain model.
The node-voltage and mesh-current methods used to analyze a circuit in the t-domain work in the s-domain as well.
Read more: https://wiki.answers.com/Q/Why_do_you_use_laplace_transform#ixzz27InwlzPY